Powered by glolg
Display Preferences Most Recent Entries Chatterbox Blog Links Site Statistics Category Tags About Me, Myself and Gilbert XML RSS Feed
Monday, Sep 17, 2007 - 01:14 SGT
Posted By: Gilbert

Or Twelve Angry Men

...again not scared. Actually, I just figured that mugging too much for the graduate Artificial Intelligence module wasn't going to help much, given that it's an unrestricted open-book quiz. So I reckoned, why not collect my impressions of the course and post them, in part organizing my own thoughts?

The A.I. of A.I. is still extremely far off (assuming that any top-secret underground government or evil-corporation research labs haven't made any fundamental breakthroughs), and as of now we are more interested in far simpler representations, for the reason that they are at least useful. This module focuses on Bayesian networks, which despite its unpromising pedigree of combining a celebrated mathematician's name with a technical term remains quite accessible - in the beginning at least.

Cut to the bone, Bayesian networks are just formal representations of dependencies between events. Before I lose anyone, here's a real-life example:

Let's say you have a friend, Kok, who sometimes invites people (such as Che B.) to his place to play mahjong. As might be imagined, Che B. is far more likely to drop by invited than uninvited - we observe that he goes to play nine days out of ten when Kok asks him to, and only one day out of a hundred when he is not asked. We also know that Kok has about an even chance of asking Che B. and other friends to play mahjong each day (ya they are very hiong).

Now, we can use some shorthand and let K be the event that Kok talks, and C be the event that Che B. plays mahjong. Clearly, whether C (Che B. plays mahjong) happens depends very much on K (Kok talks). We show this in a Bayesian Network by simply drawing two circles to represent K and C, and an arrow from K to C since K directly affects C (i.e. C is conditional on K).


Thus, "if Kok can talk, Che B. can play mahjong"

Please do not misinterpret this as saying that C can only happen when K happens. It only says that K happening or not may make a difference on how likely C is to happen. We can state exactly how likely as follows:


With probability information

In probability theory, the probability of any event E is written as P(E). If that event is bound to happen, P(E) has a value of 1. If that event is impossible, P(E) has a value of 0. In reality, most events fall somewhere in between - as may be expected, events that are as likely to happen as not to happen, like flipping a fair coin and getting heads, have a value of 0.5. E' refers to E not happening, such that P(E') = 1-P(E). Finally, P(E|F) refers to the probability of E happening if F happens.

So, from the above (very simple) Bayesian network, one can derive a number of results.

Say that, without knowing if Kok has talked today, we want to estimate how likely Che B. is to go over for mahjong. The Bayesian network tells us that Kok has been known to be equally likely to talk as not to talk, so we can base our prediction on that and weigh our decision evenly on his having talked. In this case, P(C) is P(C|K)P(K) + P(C|K')P(K'), which may be translated as "the chance that Che B. plays mahjong, is equal to the [chance that Che B. plays mahjong given that Kok talks multiplied by the chance that Kok talks] plus the [chance that Che B. plays mahjong given that Kok does not talk multiplied by the chance that Kok does not talk]". Logical? So it is (0.5*0.9)+(0.5*0.01)=0.455.

Now say that we know that Kok has talked today. Then we can ignore the possibility that he has not talked, and evaluate Che B.'s mahjong chances as 1*0.9 = 0.9 (i,e, 90%). We can even go backwards and compute the chance that Kok has talked depending on Che B. being observed to play mahjong. Intuitively, Che B. playing mahjong is a very strong hint that he has been asked by Kok; More rigorously, we can use Bayes' Rule to calculate the exact value for P(K|C) using P(C), P(K) and P(C|K), which turns out to be about 0.989 - this makes sense since we know that Che B. drops by uninvited only about 1% of the time.

Yes, I know what you're probably thinking now - so what?!

So let us say that whether a mahjong game actually happens depends on having sufficient players, who each have their own probabilities of turning up depending on Kok talking: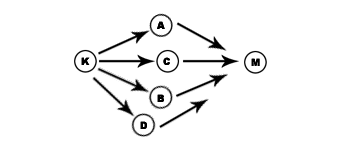


Enter Ah Seng, Bunny and Dick

...And now they influence each other on whether to go or not - Ah Seng threatens Che B., Dick calls up Bunny, and Bunny is also notified by Che B.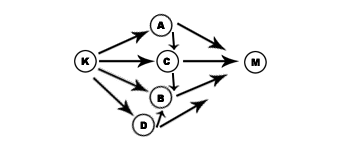


Eh, mai like that, come leh!

More of the same, and it quickly balloons far beyond human comprehension: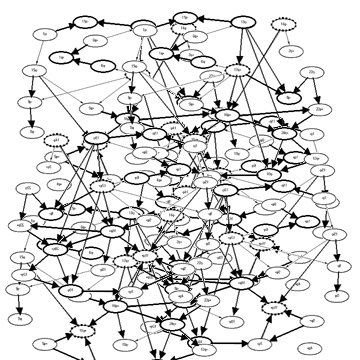


Siao liao

So here's where the indefatigable computers come in, and A.I. researchers earn their keep.


Short excerpt

The titular Twelve Angry Men came from a 1957 movie about twelve men deliberating about whether to send a man to the gallows for murder. I got to watch it for MNO, and it's one of the most riveting I've ever watched, never mind that there was no action and that almost all its one and a half hour length took part in a small jury room. All pure acting and characterization. It is fully deserving of its 100% on Rotten Tomatoes, they really don't make them like they did any more.

The kid in the movie might actually be guilty, though, and the question of reasonable doubt and justice arises - is it better to punish one innocent man together with a hundred (or whatever number of) guilty ones, or let them all go free? Another day...



comments (0) - email - share - print - direct link
trackbacks (0) - trackback url


Next: Genuinely Immaterial


Related Posts:
Economics Thus Far
On the Theory of Games
All Crocs Go To Heaven
The World of The Game
A Procrastinator Am I
Back to top

Copyright © 2006-2025 GLYS. All Rights Reserved.