Powered by glolg
Display Preferences Most Recent Entries Chatterbox Blog Links Site Statistics Category Tags About Me, Myself and Gilbert XML RSS Feed
Tuesday, May 01, 2012 - 22:59 SGT
Posted By: Gilbert

- -
Labour Day Special

It seems right to do stuff on Labour Day, so here goes.


Like That Lor

One of my profs posted an article on the shortage of good computer science and engineering graduates, which noted among other things that although CS has very low unemployment rates, the U.S. in fact graduated more CS majors in 1984 than in 2009 (and even when lumped together with mathematics, it doesn't crack the top 100 most popular majors there - one university has even eliminated its entire CS department!)

[Errata 15 May 2012: The not-in-top 100 major bit probably isn't true. Mr. Ham apologizes]

Fortunately for me, CS doesn't seem to be on the chopping board here yet, with the fellows at the top even kind enough to share (some of) their vision with us, and one polytechnic graduate even went as far as to create an online appeal to get into the programme; I can't help but applaud that go-getting spirit (of course, it may get old if everybody does the same, and there's also another side to the story)

[N.B. On the topic of admissions, the NUS management department top graduate for 2011 (sic) has asked the Prime Minister on his Facebook page the reason why he was not only not admitted to a government ministry job, but had his ideas plagarized by the ministries (discretion doesn't seem his strong suit)! I wonder if the PM had expected this sort of feedback when he took valuable time off not holding the by-election for social network outreach, but quite apart from government hiring practices, why the heck is a top business graduate aiming for the civil service in the first place? Well, at least it didn't get to this (though it's almost certainly a joke)]

Of course, the reality isn't all roses; it is common knowledge that there aren't that many really high-paying jobs in the CS field here, with services like finance and real estate still all the rage - why slave away over a terminal, competing against imported budget coders (see, even al-Qaeda is doing outsourcing now), when one can just smile a lot and earn tens of thousands per completed transaction (or at least that's the perception)?

[N.B. Here, I have to rant about too many people wanting to get rich far more than wanting to actually do anything well. While I'm not completely against the acquisition of wealth, I have never managed to rid myself of the feeling of slight unease I get whenever I hear the phrase "passive income" (at least the do-nothing-special sort; frankly, I was sort of tempted to just apply for a HDB flat with a relative and thereby contribute to the growing bubble, but other than this being perhaps no longer possible, that boat may have sailed) - as Donkin often returns to in The History of Work, work does mean something... right? No, pumping and dumping penny stocks doesn't count as that in my eyes.]



(Original source: thefinancialfreedomfoundation.org)


The catch is that to earn a good to great salary as a programmer, one generally has to actually be a good to great (and probably creative) programmer, and sad to say a degree in CS is not an ironclad guarantee of that (one memorable post mentioned that 199 of 200 applicants for programming jobs can't write code at all, which even if exaggerated tenfold, is still scary - this divide simply can't be charmed its way out of, unlike with some other jobs)

[N.B. There are horror stories about interviewees, after having presented impeccable credentials and talked up a storm, not even being able to swap two variables; however, swapping variables without using a temporary variable seems a common enough (if probably impractical) interview question. There are several ways to achieve that, the easiest probably to let x=x+y;y=x-y;x=x-y, although there are more mindbending approaches like the XOR swap. Personally, I wouldn't put too much stock in such "tricks", cool as they may be - code may not be maintained by the original author!]

Part of the trouble, I gather, is that programming can be, make that is, unforgiving - if it doesn't compile, it doesn't, and if it compiles but produces incorrect behaviour, it is still wrong (or, if the programmer is feeling cheeky enough, a new feature). Contrast this to some other fields, where everybody's opinion must be correct in its own way, inconvenient details like displeasing facts be damned.


Data Play

The official LIBSVM tutorial describes grid search as naive but straightforward, psychologically safe and trivially parallelizable. The caveat that it itself remains a heuristic that relies on the response of the dataset to parameters being reasonably uniform should still be kept in mind, however. One can imagine a grid search of normalized unit length in each dimension returning the best accuracies in a region around the examined point [Ca,ya], but having the best parameters actually at [Cb,yb], contained within the unit square defined by points [C1..4,y1..4] which all individually return accuracies worse than [Ca,ya] and which therefore may not be discovered by the search.

Of course, this intuitively could be resolved by using a finer grid and exhaustively examining more points in the (infinite with real-numbered values) parameter space, but this would take a longer time, and as the time required grows quadratically each time grid cell length is halved, cannot be kept up forever by empirical means. From this observation, the question naturally follows: For any dataset, is there any way to (even restrictively) prove that some initial granularity of search (grid here, but can be extended to any bounding method in general) is sufficient, such that the true optimal parameters are guaranteed to be obtained within, i.e. the search must converge to the optimal parameters?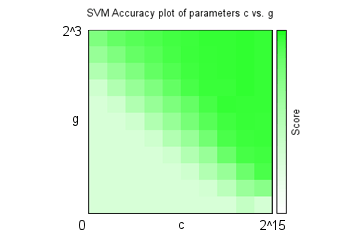


It was kind of regular for the cells, thankfully


Offhand, the answer seems to be no (excepting bounding the entire set), at least without further assumptions on the structure of the dataset. Let there be some dataset D for which grid search at some granularity G fails to uncover the optimal parameters (it might be thought of as the fine texture, or frequency, of the dataset being too small relative to the grid). Then for any given granularity G', a corresponding scaling-and-tiling R' of the original parameter response function R can be found, such that G' again does not converge to the optimal (phew, that was long-winded)

Happily, there are quite a few ways out of this. By far the most common is probably just to ignore all this and just pick some G (as I did). Farmers may not be able to prove that their agricultural technique is optimal, but that's no reason to starve, right? Those creeps are there to be last-hit, after all. I gather this does often produce good-enough solutions, and one can always examine the response over the grid to get a sense of the distribution (yes, it doesn't always work)

Another approach is perhaps to try and construct the system such that for each set of parameters, it provides a guaranteed upper and lower response bound for all points in an area around it, and therefore guarantees converging search; this is sort of related to minimax trees, with the complication that while trees in practice have a finite (often very small) number of branches, porting this to parameter space would require some proof that holds over (the infinite number of points in) an area.

Related to this is Wolpert's celebrated No Free Lunch theorem, which states that any algorithm that performs well on one problem must pay for it with poorer performance on other problems, such that their performance is in the main identical. However, this conclusion appears to follow from the observation that in the space of all possible problems, almost all of them are extremely random, and therefore no algorithm can be expected to perform particularly well on them anyway; since many scientists (and certainly businesses) are more interested in solving interesting problems, and not all of them, Wolpert's warning (which seems to have its roots in philosophy, a grounding in which does pay) would then exist as merely a curiosity to them.


The BABOON algo achieves about 70% for word recognition
(Source: wikipedia.org)


If we put aside the question of whether induction can actually be justified in practice, then an optimal solution can be defined (whew) - if the true distribution of a feature is known for multiple classes, then the minimum possible error, the Bayes error rate, is the amount of overlap between them - no algorithm can be expected to do better than that over the long run, which implies that if your features overlap greatly (and are independent), the only way to improve classification performance is to... find better features.

[N.B. Repeat warning: the true distribution may well not be Gaussian, though it seems popular to model everything as one by taking the mean and variance of training data! Well, if it's good enough... also, some distributions simply don't fit into conventional machine learning - try classifying the prime and non-prime number classes by proximity metrics only, for example]

So, is there some way to reach this optimum? In general, no, since we can only estimate the probability distributions on natural data. However, it is comforting to know that at worst twice the Bayes error rate can be achieved with the K nearest neighbour (knn) algorithm (which for 1-NN can be illustrated by Voronoi regions, seen here previously). And then the bad news: this guarantee only applies when the amount of data approaches infinity, and the correct parameter k has to be found. Okay...

[N.B. Interestingly, while one might then imagine k-Voronoi diagrams as the corresponding classification map of knn, its common definition isn't quite like that. While we're on points, I might as well mention the extremely beautiful closest pair algorithm, which non-intuitively proves that one does not have to inspect every possible pair of points to find the closest pair; then again, in practice, if the number of points (say, nodes in a network) is so great that a simple exhaustive search would take too long, I suspect that many coders would just fall back on random search, which should give acceptable results with high probability quickly]

Well, as knn happens to be Mr. Ham's favourite technique (he says it reminds him of his time at gangster finishing school, where he spent many happy hours learning to chain vulgarities together in soporific magnificence, obeying strict rules of metre and rhyme), I spent a bit of time implementing it (another of its attractions is that it can easily be coded from scratch, even on a desert island - but hmm, where would the power source come from then?) and trying it on the cell data (note that each feature has a value between 0 and 1, and thus has approximately equal influence on the "distance"):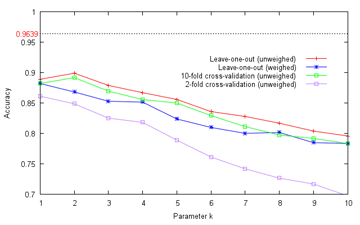




We see here that knn does not quite reach the heights (dotted line) that SVM did, which is kind of expected. Interestingly, the best results are obtained when k=1 (i.e. each cell is classified according to which other single known cell is closest to it in feature space) and k=2, depending on validation approach, which seems to indicate that fitting tightly is the way to go for this dataset (supported by good regularization parameter values found to be high for SVM, which has its tradeoffs)

Mr. Ham: KNN!

When an additional 22 noise features, each randomly assigned a value chosen with uniform distribution between 0 and 1, are added to the 22 real features, leave-one-out accuracy drops to a poor 0.5270 at k=1, and 0.5548 at k=2. This should help persuade that bad (non-discriminative) features can easily detract from performance in practical applications.

And so how good are the chosen real features actually?

Inspired by linear discriminant analysis and Otsu's method, a crude estimation of the usefulness of each feature was obtained by computing the average between-class mean differences (which suggests how well they are spread) and average within-class variance (which suggests how tightly values are distributed within each class) of each feature: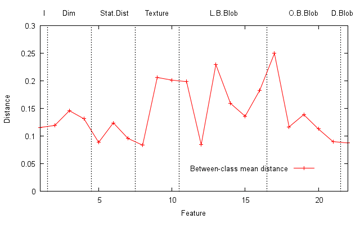


Between-class mean distances (larger should be better)


The best features by this metric are, in order, the number of small bright blobs (dots), probably due to their effectiveness in separating centromere cells, the distinctiveness of large bright blobs, due to the same for nucleolar cells, and then the self-median (texture) difference, which I believe may be a relatively new choice for this particular classification problem.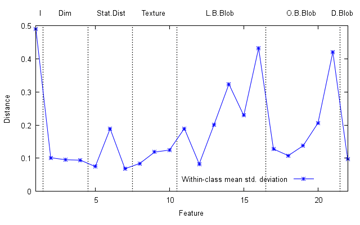


Within-class standard deviations (smaller should be better)


The most closely-clustered features happen to be the simple skewedness and mean distribution of pixel intensities, followed by the image size; unfortunately, these features are not particularly well-separated, but no matter - let SVM and knn theory do their jobs!

To end off - so how do we know which classification algorithm is the best for a particular problem? Again, the answer is, we don't. However, dedicated researchers can give it a good go by trying many of them and checking the results, whether through their own private library of scripts, or more easily with integrated data mining software like Weka, and indeed the very best performers in complex classification problems often turn out to be very specialized ensemble methods. When that happens, it may feel like black magic, but hey, if it works, it works! The end-user's certainly not complaining, after all.

It could end up working too well, such as the face detection cascade now spurring fears that Big Brother is watching everyone (it's far too late for such worries, actually), which has a NYU graduate student proposing methods to foil such systems. Unfortunately, it involves walking around looking like Lady Gaga on a bad day, and Mr. Paper Bag suggested that his longtime favourite solution could be less embarassing.


We Chinese do have built-in face recognition resistance (explained)
(Source: funnyreign.com)




comments (0) - email - share - print - direct link
trackbacks (0) - trackback url


Next: Fixy Fixed


Related Posts:
Midweek Update On Data Cells
Recognizing News
All The Same
Algo Brüno Championleagueo
The Hundred Thousand
Back to top

Copyright © 2006-2025 GLYS. All Rights Reserved.