|
| |
|
| |
|
|







|
|
TCHS 4O 2000 [4o's nonsense] alvinny [2] - csq - edchong jenming - joseph - law meepok - mingqi - pea pengkian [2] - qwergopot - woof xinghao - zhengyu HCJC 01S60 [understated sixzero] andy - edwin - jack jiaqi - peter - rex serena SAF 21SA khenghui - jiaming - jinrui [2] ritchie - vicknesh - zhenhao Others Lwei [2] - shaowei - website links - Alien Loves Predator BloggerSG Cute Overload! Cyanide and Happiness Daily Bunny Hamleto Hattrick Magic: The Gathering The Onion The Order of the Stick Perry Bible Fellowship PvP Online Soccernet Sluggy Freelance The Students' Sketchpad Talk Rock Talking Cock.com Tom the Dancing Bug Wikipedia Wulffmorgenthaler |
|
bert's blog v1.21 Powered by glolg Programmed with Perl 5.6.1 on Apache/1.3.27 (Red Hat Linux) best viewed at 1024 x 768 resolution on Internet Explorer 6.0+ or Mozilla Firefox 1.5+ entry views: 1878 today's page views: 131 (11 mobile) all-time page views: 3242729 most viewed entry: 18739 views most commented entry: 14 comments number of entries: 1214 page created Wed Apr 9, 2025 09:21:33 |
|
- tagcloud - academics [70] art [8] changelog [49] current events [36] cute stuff [12] gaming [11] music [8] outings [16] philosophy [10] poetry [4] programming [15] rants [5] reviews [8] sport [37] travel [19] work [3] miscellaneous [75] |
|
- category tags - academics art changelog current events cute stuff gaming miscellaneous music outings philosophy poetry programming rants reviews sport travel work tags in total: 386 |

| ||
|
A trusty Yahoo Groups repository for the EPL Man vs. Ham Challenge has been created, with the message timestamps proving that the predictions were made before the fact; this also unties the pretend punting from the blog, which has in the past resulted in unpolished (if punctual) posts, simply to get predictions up before the matches began. For this week, Mr. Ham bet on West Ham to beat Swansea, and had a long shot on Fulham to beat Manchester United, both of which did not come to pass; for FAKEBERT, his bets on Everton to beat Aston Villa and Norwich City to draw QPR both came off handsomely, while Liverpool held Manchester City to prevent a sweep - however, this still means that he nearly doubled his stake yet again and is sitting on 390 seeds from 200, in contrast to the winless and fuming Mr. Ham. Memories Flooded Back  (Source: facebook.com) Crap, Can't Complain Anymore A man in China built his own bionic arms (with his feet) after losing them in an accident involving explosives (it did take him eight years). As captioned by a reader of the Daily Mail: Tony Stark: I made a robot suit with my own bare hands in a cave. Sun Jifa: Dude. Please. Not all D.I.Y projects are that successful, nor all long waits that rewarding, sadly. Did randomly wander to survivalist forums and read up on how much land is needed to support a person - one acre (slightly less than a football field) seems doable, while the experienced can reap about 30 tons (!) from a plot of that size. We'll have to reach about that level of efficiency if the worst comes to pass, with only some 3% an acre per person available here in the best case - WW2-era tapioca-farming probably won't be enough any longer. The Other Armstrongs Lance got busted (or more precisely, chose not to defend against the accusations) for doping, a sad blemish on an erstwhile legend (to his detractors, anyway). On one side, he has not (officially) failed any blood or urine tests, but on the other, there were supposedly many ways around the testing, there might have been actual failures (after the experiments caught up with the drugs), and basically so many top cyclists were doping that managing to win without doing so would have been positively superhuman. Frankly, all this periodic exposing of heroes can get tiring, since it seems that a large part of whether they get caught rests on how good their doctors/advanced their drugs are. Where there's money to be made and the opportunity to raise one's chances of making it, is it any surprise that those opportunities will be taken? Take American football, where raw size and speed is at a premium - about 6% admitted to steroid use (with presumably more not coming clean) in high school, which may be a bit too much. If doping is less prevalent in (association) football, I would gather that this is largely down to pure maximal physical ability is less a factor there (e.g. Riquelme's slick if not particularly quick style) In even worse news, Neil Armstrong has left this world again. When will they be done with dagnabit rovers, and put somebody on Mars? Good luck to you too, Mr. Armstrong. Foot Went Through Entire Gastrointestinal Tract - Rep. Todd Akin, on permissible abortion When even Republicans turn on one of their own for faulty logic, you know it's a really bad mistake. Thing is, I'm convinced Mr. Akin isn't even an outright evil man - he just makes up his evidence to support his desired positions, which while not unknown, has found particular expression in the GOP (note that I dislike wanton abortion myself) Read for the week, on this note, is The Irrational Atheist: Dissecting the Unholy Trinity of Dawkins, Harris, And Hitchens (see preview), for a look at the other side. Unfortunately, while the author is witty enough, there is precious little actual content that does not involve either ad hominem attacks (though to be fair, Hitchens does hit low sometimes) or nitpicking (see detailed refutation) The Business of Tuition In this month's example of how not to go about entrepreneurship, a tutor got into trouble for presenting false credentials. Well, a self-professed "major in Double Mathematics" should have rung some bells, the only university that offers it being in Africa. Now, it could have been a honest oversight - but it then transpired that he was not a university graduate at all, was never in the Gifted Education Programme (GEP), whatever that actually counts for (but it's his mum's fault for misremembering), and has not taught at ACS Primary, which seems to be his latest invention after his GEP claims were demolished. All in all, a quite incredible story. The strange thing is, having seen a few pages of his textbook, it isn't that bad (though it should be said that authoring a primary school mathematics textbook isn't exactly a Herculean task), so he could have made a very decent living had he just kept his head down, not made the outlandish claims (which indicate very little about his teaching skills actually) and charged a reasonable fee, which is not over S$200 an hour per student in this case. I don't think he was lying when he boasted of being featured seven times in the local news, though, given mainstream journalistic standards (which did finally catch up to him in the end) Mr. Ham: Look here, the big question is, you're actually a double major in applied mathematics and a GEP kiddo, so why aren't you out there making thousand of dollars a session and buying exotic feed for me? Me: There is this little thing called a mimimum level of integrity, and anyway I turned the GEP down as I wanted to stay at my primary school, not that it did me any harm, mind. Cramming for the GEP is probably a bad idea in the first place. Mr. Ham: But think of the possibilities! See, you teach the kids a few tricks, or play Xbox with them when their parents aren't looking, and their parents willingly pay you money, and heck, the kids might even absorb something in the meantime! Everybody wins! Me: Hmm... Transformers! Following on Mr. Ham's suggestion, I gathered the hams in an attempt to explain the computing/mathematical concepts of Fourier analysis and Eigenfaces, among others, as concisely and quickly as possible, such that they might be able to discuss the topics over a dinner table in a broad liberal-artsy manner without embarrassing themselves. While I did obtain a fairly well-regarded introduction to Fourier Transforms, it was still 130 pages long and chockful of dense equations. The sharing session did not get off to the best of starts when I walked in on Mr. Ham fixated on photos of cute chicks wearing nothing but hats, which he hastily explained away as being a venerable tradition in image processing. Mr. Ham: *reseating his hat* Ok, let's get started, per the guide. No math involved, as agreed, human? Me: As little as can be managed. Now, first the idea of a transform. Here, we view it as a way to represent data in another way, possibly to emphasize some other aspect of the data. A simple example is a histogram, which shows the distribution of intensities over an image, with plenty of dark pixels in the example below - though note that an image generally cannot be retrieved from its intensity histogram. 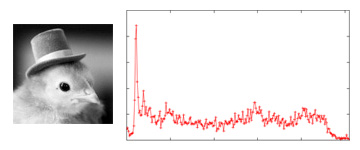 (Original source: buzzfeed.com) (Original source: buzzfeed.com)Now, Fourier analysis - you do know what sine and cosine waves are, right? Mr. Ham: Back in my very short days of formal schooling, I referred to them as "those squiggly things", then tried to patent them so that the other kids had to pay me each time they drew them; stupid teacher refused. Me: That'll do. Now, Joseph Fourier, back in the first half of the nineteenth century, discovered that complicated-looking waves could be expressed as the sums of pairs of sine-and-cosine waves, each pair at a fixed multiple of its fundamental frequency, which is just the lowest frequency in the original wave. The summation is, fittingly, called the Fourier series. 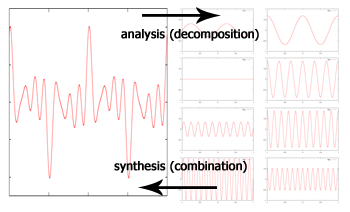 The important thing to note is that the coefficients of each of the component curves, or simply how strongly they appear in the original curve, can be computed - often by hand, through integration etc, if the original function is relatively simple, or by a computer algorithm otherwise (which is probably more common in practical applications). This process is called Fourier analysis, and the (rather simpler) inverse, of summing together the component curves, Fourier synthesis. Now, the actual process of analysis is the Fourier transform. While the math can be scary, the intuition can be fairly simple - for each frequency level, a measure is taken of how well the original signal conforms to that frequency. Take this signal - what is its frequency? Mr. Robo: It's quite clearly 3 Hertz. Mr. Ham: Five is my number of the day, so says my horoscope, so I'll go with five. 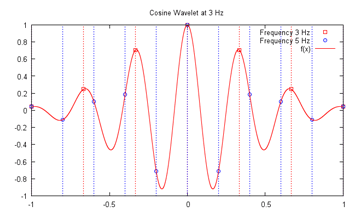 Me: As it turns out, three is the correct answer; observing the red dotted lines spaced at 3 Hz intervals, they all correspond to peaks in the signal, whereas the blue dotted lines at 5 Hz display no consistency in their intersections. We can therefore say that the 3 Hz component is very strongly represented in the signal (because, well, it is the signal in this case), while the 5 Hz (and other) components are very weakly represented. But what about, say, 3.01 Hz? While it is not as ideal a guess as 3 Hz precisely, it remains a far better guess than 5 Hz, and this is represented in the graph of the Fourier transform. As noted in the book, nice continuous functions can be rare in real life; quite often, obtained values are discretized by sampling, which gives rise to the discrete Fourier transform, which can be efficiently computed using the fast Fourier transform algorithm. Note that while the number of decompositions may be infinite in theory, roughly 30 component signals often suffice in practice (coincidentally coinciding with the statistical rule of thumb). One other thing to remember is that if insufficiently high frequencies are considered in the decomposition, some frequencies may be mistakenly recognized as lower frequencies than they actually are (see aliasing). The solution is then to decompose to at least twice the highest frequency actually present (the Nyquist frequency), which in a discrete system, is just the sampling frequency. The extension to more dimensions is straightforward, and therefore an image - which can be seen as a 2D signal - can be decomposed by a 2D Fourier transform. There are other interesting properties of the Fourier transform, such as the inversion (to retrieve the original signal from its Fourier transform) having exactly the same form as the transform itself, and therefore able to be implemented in much the same way, but the above should constitute a fair introduction on what Fourier analysis means. How to perform (or write a program to perform) it is another thing altogether, especially for real-life problems, but there are so many specialized considerations that it is probably wise to just pick up a good custom library to do it as and when required. Mr. Ham: I think I sort of understand. Me: Great, so quickly on to eigenwhatevers. Quickly now, how many dimensions are there in an image of 100 pixels each side, when considered for principal component analysis? Mr. Ham: I know! I know! Two - length and width. Take that, you know-it-all Mr. Robo! Mr. Robo: Erm, 10000? Each pixel is independent of each other pixel, and therefore is a dimension on its own. Me: Mr. Robo is, again, correct. However, it is true if seldom noted that with N possible intensity values, an image can naturally be considered as one-dimensional in a number system of base N - just that the values would be huge and admit little meaningful analysis. Mr. Ham: Then why not two dimensions? Mr. Robo: Well, it could be done by partitioning the image into two parts and expressing each part as one dimension. However, if you insist on having one dimension represent all the rows and the other the columns, the dimensions would not be independent without extra work - for example, if the row-dimension has zero value, the column-dimension is also forced to be zero. So you're still wrong, unless you can come up with another proof, but I doubt it. Me: Mr. Ham, the rear naked choke does not constitute a valid rigorous mathematical proof! Mr. Ham: Oh. My bad. *Mr. Robo slumps to floor* Me: Ok, I get it. Speeding up, recall that an eigenvector of a matrix is a vector that, when multiplied by that matrix, returns another vector that is parallel to itself. As for the applications, consider a dataset of points in many dimensions. I once had a teacher who was able to visualize something like a dozen dimensions, but for the rest of us mere mortals, three is a stretch, and as we have just seen, even a tiny thumbnail image can have ten thousand of them. Clearly, for purposes of analysis, it might be useful to reduce the number of available dimensions.  Data can reveal different things from different perspectives - here, 3D data (objects) are reduced to 2D from various angles (Original source: wikipedia.org) It may be that some particular dimensions have values that never vary (say the border of a set of cropped images), but even if this is not the case, we might wish to disregard dimensions with very little variance, but in a clever way. Consider the smallest meaningful case with two dimensions - if we wanted to express the data in one dimension, what is the best way to go about it? Mr. Robo: *groggily* Pro...project along the vector with the largest variance, creating a "shadow"? 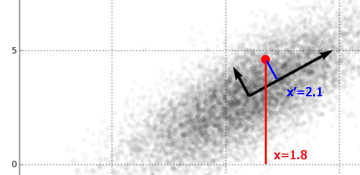 (Original source: wikipedia.org) Me: Right there you are - adapting a 2D example from Wikipedia above, the first principal component, or eigenvector with the largest eigenvalue, is along the "long edge" of the oval-shaped cloud of points. Intuitively, projecting in this direction would allow maximum variation to be accounted for - note that variance does not always correspond to range! The key idea is, again, not too difficult, though the execution may be complicated, especially with many dimensions - for a set of data in D dimensions, the first principal component is the vector representing the largest variance, as described. Since all eigenvectors have to be mutually orthogonal - sort of everywhere perpendicular - to each other, this leaves D-1 possible eigenvectors (try to visualise the case of a cube), of which the one representing the largest remaining variance is the second principal component, and so on. The use of this decomposition in practice is that even where there are many thousands of dimensions, often only a relatively very small number of eigenvectors can account for much of the variation. On to a working demo - note that each of the eigenvectors has the same dimensionality as each of the data points - hence, for a 10000-dimension image, each of the eigenvectors too has 10000 dimensions, and can therefore be expressed as an image itself. In the following example, the eigenface images were computed from a set of ten images of 92x112 pixels (from here), or 10304 dimensions.  (Original source: Face Recognition using Principal Component Analysis by Kyungnam Kim, hosted at umaics.umd.edu) Using only some combination of the topmost few eigenfaces, the original images can be retrieved (if not perfectly, see for example the rightmost girl). So what is the implication of this? Well, for one, let us say that we have a large database of a million faces. Then, if we were to save these faces naively, using one byte for each pixel/dimension, we would require about 10 gigabytes of storage space. Now, instead, let us suppose that we compute the top 100 eigenfaces, and then express each of the million images as a combination of those eigenfaces; then, the eigenfaces themselves would take up about 1MB, and with only 100 bytes (corresponding to the 100 eigenface coefficients A0 to A99) required for each face image, the total storage required would only be about 100MB - a hundredfold savings. This mostly works due to faces generally being reasonably similar from a fixed viewpoint, such that a new face can usually be largely expressed as some combination of (preprocessed) existing ones, in analogy to the Fourier decomposition of a signal into (relatively few) component frequencies. The reconstruction is rarely exact but often good enough, and the loss in quality can be quantified through measures such as signal-to-noise ratio, or more modern improvements such as the structural similarity index. The limitation then is that non-faces cannot be reconstructed from the set of specialized eigenfaces, and therefore a more universal transform is required for general usage - the common JPEG compression uses the discrete cosine transform, for instance, and there are many transformation schemes - non-negative matrix factorization for one, discrete wavelet transform for another - each with its own sets of advantages and disadvantages, but adhering to mostly the same fundamental ideas. Mr. Robo: But how do we get the eigenvectors and eigenvalues? Me: As with the Fourier transform, it's complex and somewhat out of scope here, and probably best left to prewritten code - fire up your copy of MATLAB - for real applications, i.e. not 2D toy problems, for almost all of us. Possibilities include the QR algorithm, brought up by colin during a Game of Thrones/Agricola board games session, though to be honest the theory is very seldom revisited after a module is passed. Next: Packed Up
Trackback by smart pc fixer licencia
Trackback by smart pc fixer licencia
Trackback by tuneup utilities 2013 product key
|
||||||||||||||
 Copyright © 2006-2025 GLYS. All Rights Reserved. |
||||||||||||||