|
| |
|
| |
|
|







|
|
TCHS 4O 2000 [4o's nonsense] alvinny [2] - csq - edchong jenming - joseph - law meepok - mingqi - pea pengkian [2] - qwergopot - woof xinghao - zhengyu HCJC 01S60 [understated sixzero] andy - edwin - jack jiaqi - peter - rex serena SAF 21SA khenghui - jiaming - jinrui [2] ritchie - vicknesh - zhenhao Others Lwei [2] - shaowei - website links - Alien Loves Predator BloggerSG Cute Overload! Cyanide and Happiness Daily Bunny Hamleto Hattrick Magic: The Gathering The Onion The Order of the Stick Perry Bible Fellowship PvP Online Soccernet Sluggy Freelance The Students' Sketchpad Talk Rock Talking Cock.com Tom the Dancing Bug Wikipedia Wulffmorgenthaler |
|
bert's blog v1.21 Powered by glolg Programmed with Perl 5.6.1 on Apache/1.3.27 (Red Hat Linux) best viewed at 1024 x 768 resolution on Internet Explorer 6.0+ or Mozilla Firefox 1.5+ entry views: 1073 today's page views: 459 (19 mobile) all-time page views: 3247679 most viewed entry: 18739 views most commented entry: 14 comments number of entries: 1214 page created Sat Apr 19, 2025 13:24:51 |
|
- tagcloud - academics [70] art [8] changelog [49] current events [36] cute stuff [12] gaming [11] music [8] outings [16] philosophy [10] poetry [4] programming [15] rants [5] reviews [8] sport [37] travel [19] work [3] miscellaneous [75] |
|
- category tags - academics art changelog current events cute stuff gaming miscellaneous music outings philosophy poetry programming rants reviews sport travel work tags in total: 386 |

| ||
|
As foreshadowed in the previous post, an interesting problem (apparently for an interview for a quant job), second hand from our man at Stanford, after some cosmetic adjustments from Mr. Ham and the newly-empowered Mr. Robo:
Mr. Robo was fast to come up with an attempt at an answer: First, we state some obvious crap:
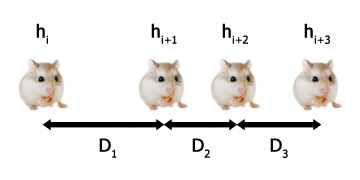 Take me home, hamster road (Original image source: singapore.gumtree.sg) Now consider any sequence of four consecutive hamsters ..., hi, hi+1, hi+2, hi+3, ... somewhere within the line of hamsters. Define the respective distances between them as D1, D2 and D3. There are then six possible permutations of distances: D1, D3, D2 D2, D1, D3 D2, D3, D1 D3, D1, D2 D3, D2, D1 Properly assuming a uniform distribution of hamsters, due to their egalitarian sensibilities, expectations E(D1) = E(D2) = E(D3), so each of these permutations are equally probable. We now consider only those (three) permutations where hi+1 is closer to hi+2 than it is to hi, i.e. D2 < D1: D2, D3, D1 D3, D2, D1 ...and we can note that in two of the three equally-likely cases, D2 < D3 too (feels kind of Monty Hall-lish). Or in other words:
...justified as the mutually-nearest neighbour property of the middle two hamsters hi+1 and hi+2 depends only (locally) on themselves and their other two neighbours hi and hi+3. And since the theohams apply independently for all hamsters (well, excepting maybe the boundary hamsters, but as the newly-assertive Mr. Robo said, who cares, n is big - or if not, Mr. Ham will make it so), the desired solution is simply 2n/3, and we are done. The question is - is Mr. Robo correct? Entirely Unnecessary Elucidation A popular recourse is of course simulation, and the average of thousand iterations with a thousand hamsters suggests strongly that the solution, if not correct, is pretty dang close (simulated result: 0.666116), and moreover pirated the first half of A Midsummer Night's Dream under Mr. Ham's purview. [N.B. Simulating with larger numbers of hamsters requires special handling of the limitations of numerical precision and random number generators, not to mention the smell] As a sidenote, it may be interesting to note that the possible number of mutually-nearest hamsters can range from all n (or at least n-1, when n is odd), down to just two. An example of all n hamsters satisfying the property would be spacing n/2 of the hamsters at a uniform distance d/(n/2+1) from each other, then assigning each of these hamsters a (mutually) nearest neighbour a distance ϵ << d/(n/2+1) away. An example of only two hamsters satisfying the property would come from placing the first hamster halfway along the road, then the second hamster halfway between the first hamster and the further end of the road, and so on for all hamsters; then, no matter how many hamsters there are, only the last two hamsters would be mutually nearest. It could also be noted that, as already mentioned by our resident math expert, the expectation of 2/3 does not hold when n=2 (since the two hamsters must necessarily be each others' nearest neighbours) The expectation does hold when n=3, from the observation that the middle hamster must have either its left or right hamster as its nearest, and that hamster must necessarily have the middle hamster as its own nearest, and therefore exactly two of the three hamsters are always mutually nearest. It also holds when n=4, from an exhaustive enumeration like that leading to Theoham One - in two of the six permutations, the first two and the last two hamsters are respectively mutually nearest, while in the other four permutations, only two of the four hamsters are as such. There is probably no reason why similarly direct proofs cannot be constructed for n=5 and beyond, though a rigorous inductive unification has so far eluded Mr. Robo. But, as the redoubtable Mr. Ham shall shortly explain, that was probably not the point of it at all. Mr. Ham Talks Sense Mr. Ham: See, this was an interview question. The whole idea was to give an answer, and get closer to snagging the job, m'kay? And let's be frank, coming up with the correct answer, as we have seen, wasn't that hard at all. It could have been done the Mr. Robo way, with his three fancy theohams, but then even I, presently a Cult Leader, can understand them, so any sciency grad student should too. Worst come to worst, one would expect the interviewee to at least figure out the answers for n=3 and/or n=4 by common sense, at a bare minimum. In any of these cases, the interviewee would have gotten the right answer. The only way not to get it was either to be so dumb as to not even be able to construct the smallest meaningful special case, or so lacking in confidence as to not want to stick his paw out after that. Ok, so he might not be able to prove to a math professor's satisfaction that it is right, but remember the job being applied for. It's a quant job. A job where, in case you weren't aware, you create theories and algorithms to rake in the cash. Fine, you might take pride in them being internally consistent, but the only place they're gonna be used is externally, interacting in unimaginably complex ways against countless other models created by competitor quants, all of whom think they're smarter than ya. And if any quant thinks that such a state of affairs can be unilaterally rendered safe, and that he can even prove it, maybe he can consider assembling a nuclear warhead where the other fellows involved are adversaries instead of collaborators - he either has a suicidally high opinion of himself, or is criminally naive. *Mr. Ham inhales on his cigar* No, the name of the game as a quant is to bluster through as far as yer can with pages of impressive-looking formulas and code, and grab as much dough as yer able to before the whole party blows up again, same as it always was. And if ya gonna let a roadful of hamsters stop ya, maybe ya not cut out for yer fistful of dollars after all. Next: The Irony Of Eden
anonymous said... Oh, got one more addition to the problem. There is a constraint. The individual probabilities are not i.i.d The road is of fixed length L. So, the probabilities are actually conditional.
Mr. Robo said... Huh but why does having a fixed, finite range mean that the variables generated cannot be i.i.d leh
anonymous said... Cuz there is a certain length that has to be always obtained in total when you sum up all the x. So, probability of getting any length is always conditional on the previous lengths
anonymous said... The solutions converge for large n because the fluctuations become smaller, and the conditional terms become weaker, but it's not an exact solution. The exact solution is actually still 2 over 3 n. In your case, actually, you can even go further and say that the exact soltuion is Twothirds x (n-2) + Half x 2 to account for the end cases but that's not the correct solution because they are not independent. And wa, why your comment box dun allow math symbols
Mr. Robo said... Well, Mr. Ham's not that hot on math, so no funding to upgrade the comment box. But I think I get what you mean. In the notation used, the absolute distances D may indeed be dependant on n the total number of hamsters, but the positions h of the hamsters remain completely independent of n. Of course, if you "observe" the D values sequentially given the positions of the hamsters, then the expectation of later D values will be conditional on earlier observations. For example, in the case n=4, if the distance between the first two hamsters happens to be large (say 0.5 for a road of unit length), the distance between the second and third hamsters is expected to be relatively small (in fact, less than 0.25) However, the claim of the expectation not actually being 2n/3, but only converging for large n, may warrant a little more clarification. A first objection is because the expectation is clearly exactly 2n/3 for n=3, and while a single case does not prove anything, it may justify further questioning. This is not so obvious for n=4, but by a million generations of four i.i.d points drawn uniformly and taking the three distances between consecutive points/hamsters, it seems extremely likely that the expectation of the distances is equal. If so, from the permutation argument, the expectation is again exactly 2n/3, and further simulation for increasing n strongly suggests that even for small n, the n-1 distances between the n hamsters indeed have equal expectations. This may be informally reasoned in plain English as follows: Given n hamsters with positions i.i.d uniformally chosen on a road of unit length, it is very unlikely that the n-1 distances between them have expectation exactly 1/(n-1), since it is almost certain that the first hamster is not exactly at distance zero, and the last hamster is not exactly at distance one. However, given the actual observed positions of the first and last hamster, I, Mr. Robo, argue that for all n>2, the expectation of the n-1 distances are all exactly (last-first)/(n-1) (and are thus also equal). This is as the distribution of the positions of the remaining n-2 hamsters remains uniform over the range (first,last), or more mathily E(D1|first,last) = E(D2|first,last) = ... = E(Dn-1|first,last), and in practice we compute E(Di|{positions of all hamsters}) If the expectation values for distances are indeed equal, the permutation argument is sufficient, and for the 24 permutations with n=5, eight of them have four mutually nearest hamsters, and the remaining 16 have two, again for an expectation of exactly 2n/3 [see code]: 1 (4 3 2 1) -> 2 ...to give 80/120 mutually closest hamsters over all permutations. The same holds for the following values of n: n=6: 480/720 n=7: 3360/5040 n=8: 26880/40320 n=9: 241920/362880 ...and there is no reason why it cannot hold indefinitely since all successive permutations must remain divisible by three, though I can't exactly prove it yet. [N.B. Insidious bug in original code, corrected 3rd December 2012]
anonymous said... Oh, I was actually saying the answer is exactly Two-third n, but your derivation in the blog post neglects mention of the end cases, and that suggests a derivation that is entirely dependent only on large n, (i.e. end cases are neglected.) Additionally, your earlier solution was a claim dependent on the actual independence of the individual distances, which is not true. On the other hand, Mr Robo's following claim: However, given the actual observed positions of the first and last hamster, I, Mr. Robo, argue that ... (and are thus also equal). is critical to your above correction to the solution. Anyway, what the interviewers were looking for was a mathematical proof to the problem, and it comes in the form of beta distributions and gamma functions. Haha, anyway, you should ask CSQ sometime about his solution. He tried explaining it to me over whatsapp, but very hard to follow, so I gave up trying after I saw my friend's solution.
Mr. Robo said... Okoj, so it was Mr. Ham who was the most mistaken. Got it. Then again, gamma functions seem related to permutations, so.
Linkback by
|
|||||||||||||||||||||||||||||
 Copyright © 2006-2025 GLYS. All Rights Reserved. |
|||||||||||||||||||||||||||||